Explaining the Many-Worlds Interpretation
(c) 2010 Kim Øyhus
(With pretty pictures)
Quantum Mechanics is difficult and confusing, and one of its interpretations
is "Many-Worlds", which says that there are lots of universes which divide
into new universes on every quantum observation, and that this is what one
gets if one take the mathematics of Quantum Mechanics as true.
I independently came to this conclusion in about 1990 when studying Quantum
Mechanics at NTH, the Norwegian Institute of Technology, which sadly does not
exist anymore. This is written in December 2009, so I waited a long time
before writing this down.
This text is about how I came to this conclusion, hopefully explained in a
good way, just like they did not explain it to me. Quantum Mechanics
explanations usually have big dead zones that most explainers avoid, mainly
because they do not understand it themselves, and are just copying others. So
textbooks tend to copy each other, almost verbatim. The few exceptions to this
I have studied myself, is Feynmans work, which admits the dead zones of
understanding exists, but give understandable explanations on how to calculate
and test, which is what is actually needed in science, and which can be used to
find out stuff about the dead zones. And then there is "Understanding Quantum
Mechanics, a User's Manual" by Michael A. Morrison, which is very good at
explaining the fundamentals, but only for one-particle systems. One must have
many-particle models to understand the many-worlds interpretation and its
connection to Quantum Collapse.
What is this Quantum Collapse really?
To calculate the probability of an event, one squares the amplitude of the
wave function.
Okay. Nice to know. But I thought events was something that could be modeled
by wave functions, not something outside of it. And if this math is true, or
at least consistent with all observations, how does it discern between events
and other stuff?
After reading some more Q.M., some of which were mandatory in my
study, some that I bought extra, and some popular science paper backs, of
which I can only recommend "Q.E.D." by Richard Feynman, I got mostly
mis-informed that this was about Observers, which somehow got
probability waves to Collapse into events.
Again Okay, nice to know, but why do they not have any mathematical model of
this collapsing stuff except the change of quantum wave into a probability
function? How does one discern an observer from other stuff in the Universe?
How does the universe do it? Is it doable at all? Does it even make sense?
After learning and using Q.M. for some years, I knew the calculations
were done without any regard to any observer, except as some sort of
process at the end of experimental quantum processes. It was really
weird that physicists did not show any particular interest in this
collapse process, but instead treated it as a sort of taboo. I finally
got hold of articles about Bell, Aspect, and their experiments, which
I did not understand at the time, because I had not learned
many-particle Q.M., which unfortunately was rather badly taught, both
in lectures and in books. But I got the point that one had to use
many-particle models to understand this.
What is a Quantum Observer anyway?
All I got was that they were kind of magical, not described by math, avoided
by physicists because of shame of unphysicality or something.
But fortunately, I knew computer science, which most physicists do not
know, with the Church-Turing thesis, which roughly states that
anything physical can be simulated by a computer. This means that
observers can be simulated by a computer. So all I had to do to put
observers into the math was to simulate a universal computer that
observes quantum collapsing in its own little universe. To do this, I
had to understand many-particle Q.M.
The difficult thing about many-particle quantum mechanics, in addition
to understanding it, is that its wave function gets 3 dimensions for
each particle, so it gets difficult to visualise and understand even
for just 2 particles since they need 6 dimensions. To make the model
comprehensible, and possible to visualise, I had to simplify it as
much as possible, and I reduced it to just two dimensions, in addition
to time, so the model can be visualised as a picture evolving in time,
and shown here.
Pictures of this are further down in this article. You can also
try a simulation in
java.
A superposition
If we look at a superposition of a live and dead cat, why do we not see a sort
of double exposure picture? According to many people, that is what we should
see if quantum mechanics were right, and the collapse of the wave function is
what stops that from happening.
But cats are far too big to model mathematically, so I went for the simplest
superposition I could find: One particle moving along a line, and having a 50%
chance of being reflected at a barrier on this line. This is in practice a half
silvered mirror, except that it is only one dimensional, and the particle can
be an electron, and the mirror a positive potential. After hitting the
potential the particle will be in a superposition of being bounced back, and
continuing forward.
This is similar to an electron in a thin wire with a small gap.
An observation
When the reflected electron passes by, what will it be like to observe it?
- 1. It will be like an electron that is half there.
- 2. The math will collapse, just as reality, and it will either be there
fully, or not.
- 3. The observer will get into a superposition of seeing the electron
fully, or not at all.
- 4. Something different from the above.
Which one of these claims is true according to the math?
So, to test this, the observer and math must be able to discern between at
least these four possibilities. Humans can be observers, and we have eyes that
do the observing part, and a brain that can be conscious of the
observation. Many believe that this consciousness part is causing the
collapse. If consciousness has a role, that role will happen after the eye
does the observing, and the brain will not be in a superposition yet, so if it
is sufficient to just model the eye, that should be apparent in the model, and
it was so.
Instead of an eye, I use a much simpler device: just an electron that
is in the path of the returning reflected electron. These 2 electrons
will bounce when they hit each other, so the observing electron will
move, and this movement can be further observed and amplified, thus
doing its observing by bouncing into more observed observations.
So, what could happen in the model? How will the observing electron bounce?
Here are the 4 scenarios from above:
- 1. It bounces as if hit with a particle half the charge and mass of an
electron.
- 2. The calculated wave function will somehow converge randomly to a full
bounce, or no bounce at all. Since there is no randomness in the math, this
is impossible. If this is what happens in reality, then the math of Q.M. is
wrong.
- 3. It will be in a superposition of being bounced, and not at all.
- 4. It will bounce differently from all of the above scenarios.
Since everything happens in just 1 dimension, with 2 particles, this
can be visualized as time slices of a 2 dimensional model, with full
phase space. This is a complete Hilbert space model of this quantum
mechanical system, modeled as a 2 particle Schrödinger equation, by me.
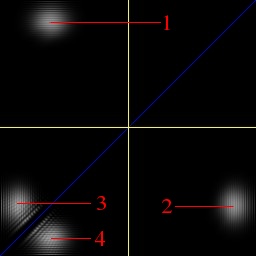
The positions of the electrons are represented by the heights of the blobs:
Both electrons are now in a superposition. That they are in
2 separate worlds can be seen by noting that the 2 probability blobs
on the same side of the diagonal, have no coordinates in common. They
are separated both horizontally and vertically. Before the
observation, but after the mirror split, they had one coordinate in
common. And before the mirror split, it was just one blob, which of
course had both of its coordinates in common with itself.
Conclusion
Possiblity 3 is the correct one:
The observer got into a superposition of seeing the electron fully, or not at all, thus confirming the "Many Worlds" interpretation.
I did not do the actual simulation before now. When I studied, I just
visualized it, but got the same answer.
To summarize what happens here:
First, one electron gets into a superposition of being in 2 places.
Then, the superposition gets to 2 electrons, being in 2 worlds, thus an observation.
If this second electron was in the retina of a human, then the
superposition would split the surrounding atoms into 2 worlds, and
then the neuron, and then the optic nerve, the brain, the entire
observer, and then the entire universe around the observer, particle
by particle, starting with the second electron. The superposition
of the first electron is thus extremely contagious.
Changelog
2010.01.04 First partial version.
2010.01.05 Proofread and a little rewritten.
2010.01.05 Some better explanations added on advice from friends.
2010.01.13 New pictures.
Any comment?
kim.oyhus@gmail.com